はじめに|G検定で数理統計が重要視される理由

G検定は、AI に関する幅広い知識を評価する試験ですが、その根幹となるのが数理統計の理解です。
最新シラバスでは「AI に必要な数理・統計知識」という独立セクションが設けられ、配点も従来より高く設定されています。
言い換えると、ここを落とすと合格ラインから一気に遠ざかります。
1 AI モデルは数式で動きます
深層学習であれ勾配ブースティングであれ、最終的にモデルを更新するエンジンは微分と最適化です。
損失関数の勾配を正しく計算してこそ、重みが目標方向へ収束します。
数学を理解していないと、ハイパーパラメータ調整が「運頼み」になりかねません。
2 データを読む力が精度を左右します
平均・中央値・分散・標準偏差といった代表値とばらつきは、外れ値処理や特徴量スケーリングの判断材料になります。
さらに「共分散・相関・擬似相関」を誤解すると、意味のない特徴を採用したり、リーケージを見落とすリスクが高まります。
3 確率思考がビジネスリスクを下げます
生成 AI の出力確率、異常検知の閾値設定、A/B テストの効果測定——すべてが確率分布と仮説検定の知識に直結します。
統計的に有意かどうかを判断できなければ、意思決定が感覚的になり、プロジェクト失敗の温床となります。
4 距離尺度と類似度は応用範囲が広いです
クラスタリングやレコメンドでは「ユークリッド距離」と「コサイン類似度」を適切に選ぶことで精度が大きく変わります。
多変量データでは「マハラノビス距離」が外れ値検知の決め手になります。
距離の選定=モデル性能と言っても過言ではありません。
本記事では、G検定の出題傾向を踏まえつつ、最小限の公式と最大限の実務応用を結び付けて解説します。
数式が苦手な方でも理解しやすいよう、図解イメージと言語化ポイントを多用します。
読み終えるころには、数理統計が「得点源」から「武器」へと変わるはずです。
次章からは、まず微分と最適化の基礎を30分でマスターし、勾配降下法や確率的最適化アルゴリズムがなぜ機能するのかを直感的に掴んでいきます。
微分と最適化の基礎を30分で理解します

微分は関数の「変化率」を測る道具です。
機械学習では損失関数がどの方向へ小さくなるかを勾配(微分値)で求め、最小値へ向かってパラメータを更新します。
勾配降下法のしくみを図で把握します
- 損失関数 L(θ)を定義します。
- パラメータ θの初期値を決めます。
- 勾配 ∇θL を計算し、学習率 ηを掛けて、θ←θ−η∇θLと更新します。
- これを繰り返すと損失が最小付近へ収束します。
ポイント
- 勾配が 0 なら最小値または鞍点に到達しています。
- 学習率が大きすぎると発散し、小さすぎると収束が遅くなります。
バッチ・ミニバッチ・オンライン学習の違いを押さえます
| 手法 | データ利用 | メリット | デメリット |
|---|---|---|---|
| バッチ | 全データ | 安定・高精度 | メモリ消費が大きい |
| ミニバッチ | 小分割 | GPU 並列化・収束速い | バッチサイズ調整が必要 |
| オンライン | 1 サンプル | リアルタイム対応 | ノイズの影響が大きい |
深層学習では ミニバッチ学習+Adam がデファクトです。
Adam はモメンタムと適応学習率を組み合わせ、勾配が不安定な領域でもスムーズに収束します。
勾配消失と勾配爆発を防ぐテクニック
- 活性化関数を ReLU 系に切り替えます。
- 勾配クリッピングで勾配ノルムを上限値に制限します。
- 残差接続やバッチ正規化で勾配の流れを確保します。
二乗誤差と交差エントロピーを直感で理解します
- 二乗誤差(MSE) は回帰タスク向けで、大きな誤差に強いペナルティを与えます。
- 交差エントロピー は確率のずれを測り、分類タスクの損失として最適です。
どちらも「損失が 0 に近いほどモデルが正確」と覚え、グラフの形状と勾配の大きさをイメージすると公式暗記より早く定着します。
代表値とばらつき 平均・分散・標準偏差を使いこなします

平均・中央値・最頻値の使い分け
- 平均値 は外れ値の影響を受けやすいですが、全体傾向を把握しやすいです。
- 中央値 は外れ値に強く、収入や住宅価格のように偏りが大きいデータで有効です。
- 最頻値 はカテゴリデータや多峰性分布の代表値として使います。
分散と標準偏差で散らばりを測定します
分散はばらつきの大きさ、標準偏差は「元データと同じ単位」でばらつきを示します。
標準偏差が小さいほどデータが平均に集中し、品質が安定していると判断できます。
箱ひげ図で外れ値を可視化します
四分位範囲 (IQR) の 1.5 倍を超える点を外れ値とみなし、前処理で除外または Winsorize 処理を行います。
G検定では「外れ値を残すとモデル性能がどう変わるか」を問うケースが多いため、目的に応じた外れ値処理を説明できるようにしましょう。
確率分布と期待値 ベルヌーイから正規分布まで一気に整理します
離散型と連続型を区別します
- ベルヌーイ分布:成功確率 pp の二値試行
- 二項分布:ベルヌーイ試行を nn 回繰り返した成功回数
- ポアソン分布:希少イベント発生回数(平均 λ\lambda)
- 正規分布:平均 μ\mu、分散 σ2\sigma^2 の連続分布
正規分布は「68 % が μ±σ、95 % が μ±2σ」という経験則を覚え、異常検知の閾値設定に活用します。
期待値と分散の公式を活用します
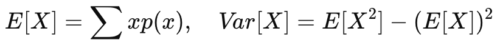
期待値は「長期平均」、分散は「平均からの散らばり」と理解すると、確率思考でリスクが直感的に見えてきます。
共分散・相関・擬似相関 データ間関係性を正しく読み解きます

共分散と相関係数の違い
- 共分散は関係の方向を示しますが、スケール依存です。
- 相関係数は −1≤r≤1 に正規化され、強さと方向を同時に示します。
擬似相関に注意
隠れた第三要因が両変数に影響していると、因果がないのに高相関となる場合があります。
年齢・収入・健康指標など多重共線性が疑われる特徴量は、偏相関係数で検証します。
仮説検定と推定 帰無仮説を立ててモデル改善を検証します
p 値の意味を誤解しない
p 値は「帰無仮説の下で観測値以上の結果が出る確率」です。
0.05 未満なら帰無仮説を棄却し、効果が「統計的に有意」と判断します。
t 検定・χ² 検定・F 検定の使い分け
| 検定 | 目的 | 例 |
|---|---|---|
| t 検定 | 平均の差 | AB テストで CVR 比較 |
| χ² 検定 | カテゴリ分布差 | 男女別購買傾向 |
| F 検定 | 分散の差 | モデル残差の比較 |
仮説検定は「効果があるか」を定量的に示す力です。
モデル改善時は 旧モデル vs 新モデル を検定し、 p 値と効果量(Cohen’s d など)を併記すると説得力が増します。
距離尺度と類似度 ユークリッド距離とコサイン類似度の実践比較
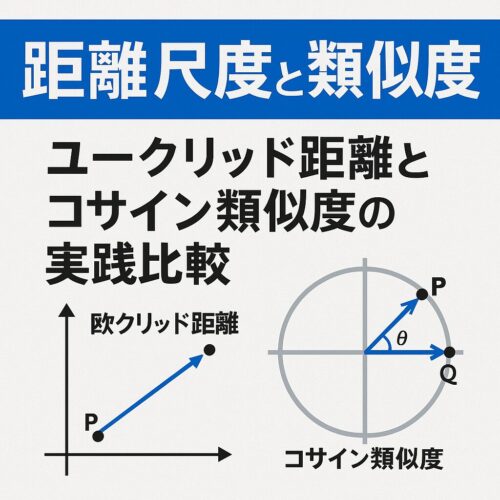
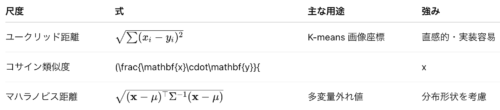
距離選定の基本は「データの性質とタスクに合うか」です。
高次元 sparse ベクトルならコサイン、一様分布でスケールが同じならユークリッド、分散構造を含む多変量ならマハラノビスを選びます。
統計指標をPythonで計算 Jupyter Notebookの活用術
import pandas as pd
import numpy as np
from scipy import stats
df = pd.read_csv("sales.csv")
mean = df["revenue"].mean()
std = df["revenue"].std()
corr = df[["ad_cost", "revenue"]].corr().iloc[0,1]
t_stat, p_val = stats.ttest_ind(df_A["cvr"], df_B["cvr"])
print(f"平均: {mean:.2f}, 標準偏差: {std:.2f}")
print(f"広告費と売上の相関係数: {corr:.2f}")
print(f"CVR の t 検定 p 値: {p_val:.4f}")
- Jupyter Notebook はコード・結果・考察を同一ファイルで共有でき、再現性とレビュー効率が向上します。
requirements.txtを添付し、環境依存を排除しましょう。
試験直前チェックリストと学習スケジュール
- 代表値・ばらつき:公式と使い分けを暗唱できますか?
- 確率分布:離散 vs 連続、ベルヌーイ・二項・正規・ポアソンを即答できますか?
- 仮説検定:帰無仮説と p 値の定義を説明できますか?
- 距離尺度:ユークリッド・コサイン・マハラノビスの適用シーンを言えますか?
- 最適化:勾配降下法の更新式と学習率の役割を理解していますか?
1 週間仕上げプラン
| 日 | 学習内容 | 目安時間 |
|---|---|---|
| 月 | 微分・最適化復習 | 1.5 h |
| 火 | 代表値・分散・標準偏差 | 1.5 h |
| 水 | 確率分布と期待値 | 1.5 h |
| 木 | 相関・擬似相関・距離 | 1.5 h |
| 金 | 仮説検定・推定 | 1.5 h |
| 土 | 過去問 160 問演習 | 3 h |
| 日 | 弱点復習・模試 | 2 h |
このスケジュールで基礎→応用→演習を高速回転させれば、数理統計セクションで8 割以上の得点が見込めます。
G検定合格を確実にし、AI プロジェクトで即戦力となる統計リテラシーを手に入れましょう。
>今回紹介したG検定の学習内容以外を学びたい方は、こちらからご覧ください👇
