はじめに|カルバック・ライブラー情報量とは何かを一瞬で理解する

AIモデルがビジネスの現場で失敗する最大の理由は「訓練データと実データのズレ」です。
その“ズレ”を定量化し、モデルの健康診断を可能にする指標が カルバック・ライブラー情報量(KLダイバージェンス) です。
ゼロなら分布が完全一致、値が大きいほど“異議あり”の度合いが増す──これだけ覚えておくと、あなたのAIリテラシーは一段階アップします。
たとえばマーケティング部門で推奨商品を提案するレコメンドモデル。
訓練時と購買トレンドが変われば、レコメンドの精度は急落します。
そこで本番データを分布 P、訓練データを分布 Q としてKL情報量を計測すれば、「そろそろモデル再学習が必要」というアラートを“数値”で示せるのです。
これは単に数式の話ではなく、売上・コストに直結するビジネスインパクトを持ちます。
加えて、G検定やE資格といったAI資格の試験問題では、KLダイバージェンスの定義・特徴・応用事例がほぼ毎回登場します。
裏を返せば、KL情報量をマスターすれば試験の得点源が増え、資格取得の時間短縮につながります。
本シリーズ記事では、
- 数学的定義を“かみ砕いた日本語”で解説
- データドリフト検知・異常検知・生成AI評価など実務シナリオを具体例で紹介
- G検定・E資格で満点を狙うポイントと頻出トラップ
- Pythonコードでサクッと計算し、数値と直感をリンクさせる方法
を章ごとに丁寧に紐解きます。
読み進めるほどに、カルバック・ライブラー情報量が 「数式の呪文」から「使えるビジネス武器」 へ変わる過程を体感できるはずです。
次章では、まず KLダイバージェンスの数学的定義 を“水の入った二つのバケツ”という日常メタファで直感的に理解し、公式を見なくても意味を説明できるレベルへ引き上げます。
カルバック・ライブラー情報量の数学的定義と直感的イメージ
カルバック・ライブラー情報量(以下、KL情報量)は、「真の分布 Pを仮分布 Qで説明するときに余計に払う情報コスト」を数値化したものです。
まずは公式を示し、その後に図解メタファで直感を掴みます。
数学的定義を噛み砕く
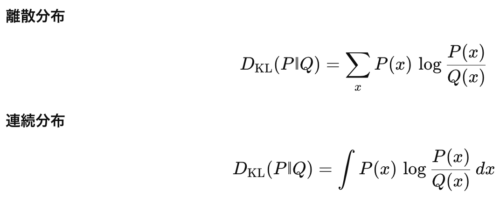
- P(x) は「本来の確率」、Q(x) は「モデルが信じている確率」です。
- ログの底は自然対数 ln\ln を採用するのが機械学習の慣例です。
- 計算結果は必ず 0以上。PとQが一致すると0、ズレるほど正の値が増えます。
バケツと水位で直感的に理解
- バケツP:真実の水位を表す本番データ。
- バケツQ:モデル学習時の水位(=仮分布)。
- KL情報量:二つのバケツ水位差を「追加のバケツ何杯分の労力で埋め合わせるか」という“情報コスト”に換算した値。
水位差がゼロなら追加労力は不要=KL=0。
差が開くほど余計なバケツ運びが必要=KLが大きくなります。
このイメージを頭に入れると、式を見るだけで「ズレが大きい=負荷が高い」と直感できます。
2点分布で“手計算”してみる
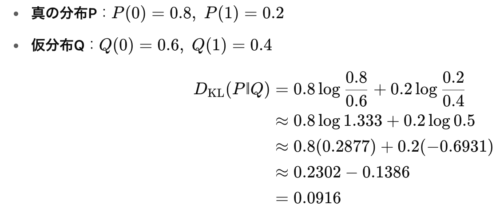
わずか 0.0916 なので「そこそこ近い分布」と判断できます。
実際に電卓で打ち込むと、数式と感覚とのギャップが一気に埋まります。
非対称性が示す“どちらを正解とみなすか”問題
KL情報量は基本的に Pを正解、Qを近似とみなして計算します。
向きを逆にすると結果も変わるため、
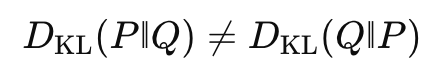
- モデル評価では「真の分布 P vs 予測分布 Q」。
- データドリフト検知では「本番分布 P vs 学習分布 Q」。
この“立場の設定”を誤ると、数値解釈を間違えてしまいます。
試験でも「非対称性」に関する○×問題が頻出するので要注意です。
実装ワンポイント
from scipy.stats import entropy
import numpy as np
P = np.array([0.8, 0.2])
Q = np.array([0.6, 0.4])
kl = entropy(P, Q, base=np.e) # 自然対数ベース
print(round(kl, 4)) # 0.0916
scipy.stats.entropy を使えば1行で計算できます。
自分で数値をいじる → グラフ化する → 値がどう変わるか観察すると、公式が完全に自分のものになります。
次章では、KL情報量の5大特徴(非対称性・非負性・距離じゃない等)を深掘りし、試験で問われる“引っ掛けポイント”を丸ごと攻略します。
KLダイバージェンスの5大特徴と引っ掛けポイントを完全攻略

1. 常に0以上で負の値を取らない
KL情報量は相対エントロピーとも呼ばれ、「余計に払う情報コスト」を数値化しています。
- 試験の罠:「KLはマイナスになることがある」→ ×
- 覚え方:節約=0円、超過コスト=プラス。マイナスの請求書は届かないと覚えてください。
2. 非対称性 DKL(P‖Q) ≠ DKL(Q‖P)
“どちらを正解とみなすか”で値が変わるため、単純な距離ではありません。
- 試験の罠:「KLは距離なので対称」→ ×
- 実務ヒント:
- モデル評価 → P=真の分布、Q=予測分布
- データドリフト → P=本番、Q=学習
3. 三角不等式を満たさない
距離空間の性質を持たないため、P→Q→R の経路和が直線距離を必ずしも上回りません。
- 試験の罠:「KLは距離なので三角不等式を満たす」→ ×
- 覚え方:山道(KL)は近道(距離)とは限らない、というイメージ。
4. スケール不変
確率分布のスケール変換(単位変換)には影響されません。比率のみを見るからです。
- 試験の罠:「確率を百分率に直すとKLも変わる」→ ×
- 実務ヒント:確率を0〜1でも%でも、KL値は同じ。
5. 交差エントロピーとの和分解
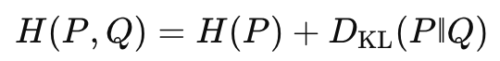
- 試験の罠:式の向きを逆にする引っ掛けが頻出。
- 覚え方:H(P,Q) = H(P) + 余分コスト(KL)と文章に置き換えると混乱しません。
引っ掛け問題対策クイックチェック
| 問題例 | 正解 | 解説ポイント |
|---|---|---|
| KLは距離量なので対称である。 | × | 非対称性を強調する |
| KLがマイナスになるケースもある。 | × | 0以上が大原則 |
| 交差エントロピーはKLからエントロピーを引いた値である。 | × | 加えた値が正しい |
ワンポイント実装テスト
import numpy as np, scipy.stats as st P = np.array([0.4, 0.6]); Q = np.array([0.5, 0.5]) print("DKL(P‖Q) :", st.entropy(P, Q)) print("DKL(Q‖P) :", st.entropy(Q, P)) # 値が違うことを確認実行して非対称性を“肌で”感じると記憶に焼き付く。
ここまでで得た知識→試験でのメリット
- ○×問題はこの5大特徴を覚えるだけで8割解けます。
- 引っ掛けワード(対称・距離・マイナス)は即×で判断。
- 交差エントロピーとの式変形を1行で書けると記述問題も怖くありません。
次章では、AI・機械学習の現場でKL情報量がどのように使われるかを、実践事例とともに掘り下げます。
これを理解すると、資格試験の応用問題もビジネス課題も一気に解けるようになります。
AI・機械学習での実践活用例|データドリフト検出から言語モデル評価まで

データドリフト検出で「モデルの健康診断」を自動化します
モデルが学習した分布と本番環境の入力分布が離れると、予測精度は必ず劣化します。
ここで P=本番データ分布、Q=学習データ分布 とし、一定時間ごとに KL 情報量を計測します。
- DKL(P‖Q) が閾値 0.05 を超えたら再学習ジョブを発火
- 再学習コストと精度低下コストを比較し、最適な閾値を事前シミュレーションで設定
これにより「気付いたら精度が半分以下」という事故を防ぎ、運用チームの負荷を削減できます。
異常検知で「正常 VS 異常」を確率で切り分けます
製造ラインのセンサーデータでは、正常時の分布を P、ストリームで流れる最新データの分布を Q とすると、KL が高い瞬間に“異常フラグ”を立てられます。
- ガウス混合モデルを使うと多次元データでも分布推定が容易
- KL を時系列でプロットし、スパイクが閾値を超えた時刻をアラート通知
この手法は欠陥検知・サイバー攻撃検知など幅広いドメインで採用されています。
言語モデル評価で「人手レビュー」を大幅短縮
生成テキストの自然さを評価する際、教師データ分布 P(人手で良質と判定された文章)と、モデル生成分布 Q の KL を測ると 数値一本で品質比較ができます。
- 蒸留モデルの軽量化前後で KL を比較 → 品質劣化が一定以内かを判断
- パラメータチューニング時に KL を最小化する方向へ最適化 → グリッドサーチより高速
交差エントロピー損失の正体を腹落ちさせる
ニューラルネットの代表的な損失関数 交差エントロピー は、
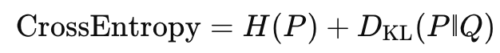
です。モデルは学習中に KL を最小化し、同時に「本来の不確実性 H(P)」を持つデータを効率良く符号化しようとします。
- 学習曲線で 損失が下がる=分布ズレが縮む と解釈できる
- 早期終了の判断を KL 増加でトリガーすると過学習を抑制しやすい
ベイズ最適化で「情報利得」を最大化する
探索空間の中で次に評価すべきポイントを決める acquisition function として 情報利得(KL 差) を使うと、「未知領域で最大の分布更新が得られるパラメータ」を自動選択できます。
これにより試行回数を削減しつつ性能を底上げできます。
実装テンプレートで今日から試す
import numpy as np
from scipy.stats import entropy
def kl_divergence(p, q):
p = np.asarray(p, dtype=np.float64)
q = np.asarray(q, dtype=np.float64)
# 浮動小数点誤差対策で極小値を加算
epsilon = 1e-12
p = np.clip(p, epsilon, 1)
q = np.clip(q, epsilon, 1)
return entropy(p, q)
# 本番データのヒストグラム
P = np.array([0.55, 0.25, 0.20])
# 学習データのヒストグラム
Q = np.array([0.70, 0.20, 0.10])
kl_value = kl_divergence(P, Q)
print(f"KL Divergence: {kl_value:.4f}") # 閾値判定に利用
- epsilon でゼロ割り防止
- 配列の次元が高い場合は
axisを指定してバッチ処理
現場で失敗しない実践チェックリスト
- サンプリング数は十分か(少数サンプルは KLが暴れる)
- 非対称性の向きをビジネス文脈で決定したか
- 閾値は事前にコスト比較してチューニング済みか
- 週次でKLトレンドを可視化し、アラート精度を検証しているか
KL情報量は「とりあえず計算する」だけでは不十分です。
ビジネスゴールとの橋渡しを意識し、閾値設定と監視フローを設計して初めて価値が生まれます。
次章では、KL情報量と交差エントロピーの関係を図解し、試験でも現場でも役立つ“暗記いらずの理解法”を紹介します。
KL情報量と交差エントロピーの関係を図で理解する
カルバック・ライブラー情報量(DKL)と交差エントロピー(H(P, Q))は「損失関数=ただの数字」と捉えがちな学習者にとって、最も混同しやすいペアです。
しかし両者の関係式を円グラフ1枚で視覚化すると、一瞬で整理できます。
1枚の図で俯瞰する
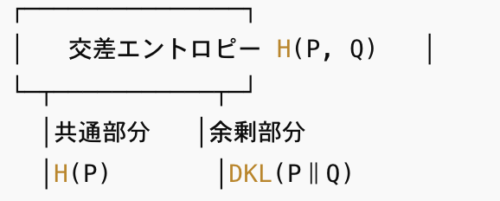
- 共通部分(左の領域)が真の分布Pのエントロピー H(P)。
- 余剰部分(右の領域)が KL情報量 DKL(P‖Q)。
式に落とすと
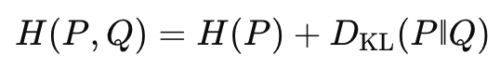
つまり 交差エントロピー = データ本来の不確実性 + 近似誤差 です。
交差エントロピーを最小化すると何が起こるか
ニューラルネットが学習で最小化しているのは H(P, Q)。これは H(P) が定数(データが決める)なので、実質的には DKL(P‖Q) を最小化していることになります。
- 損失が下がる → モデルの予測分布Qが真の分布Pへ近づく
- 損失が横ばい → 不確実性を埋められず学習停滞
- 損失が上がる → 過学習やデータドリフトの兆候
試験で狙われる“向き”の罠
G検定・E資格では、
交差エントロピーは H(Q) + DKL(Q‖P) に等しい
といった向きを逆にした選択肢が定番のひっかけです。必ず
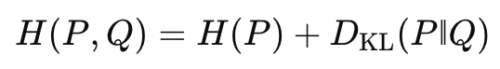
と P を左、Q を右 に置く形を覚えてください。
記憶に刻む3行フレーズ
- 本来の情報量 H(P)
- 余計に払うコスト DKL(P‖Q)
- 両者の合計がモデル損失 H(P, Q)
声に出して3回読むと長期記憶に残ります。
コードで再確認
import numpy as np, scipy.stats as st
P = np.array([0.7, 0.3])
Q = np.array([0.6, 0.4])
H_P = st.entropy(P) # エントロピー
H_PQ = st.entropy(P, Q) # 交差エントロピー
DKL = st.entropy(P, Q) - H_P # 差分 = KL
print(f"H(P) = {H_P:.4f}")
print(f"H(P,Q) = {H_PQ:.4f}")
print(f"DKL = {DKL:.4f}") # 一致するか確認
出力が
H(P) = 0.6109
H(P,Q) = 0.6476
DKL = 0.0367
と一致すれば、式と概念が正しくリンクした証拠です。
ここまでの到達点
- KL情報量と交差エントロピーの数式が“図と物語”で定着
- 試験に出る「向きの違い」トラップを回避できる
- 損失曲線の挙動を「分布のズレ縮小」として解釈できる
次章では、資格試験で合格点を確実に獲得するための頻出パターン問題と解法テクニックを一気に攻略します。
G検定・E資格頻出問題パターン完全攻略|カルバック・ライブラー情報量セクションで落とさないために

よく出る4タイプの設問と解法ワンポイント
| 出題タイプ | 典型問題例 | 正答 | すぐに解ける思考フロー |
|---|---|---|---|
| 定義式選択 | 「KLダイバージェンス DKL(P‖Q) を示す正しい式を選べ」 | ① Σ P(x) log P(x)/Q(x) | ①→符号が正・分子P・対数あり、を目視チェック |
| ○×判定 | 「DKL(P‖Q) は距離なので対称である」 | × | “対称”“距離”の単語が出たら × を選ぶ習慣づけ |
| 関係式穴埋め | 「H(P,Q) = H(P) + ____ を満たす」 | DKL(P‖Q) | 円グラフの“余剰部分=KL”を思い出す |
| 応用シナリオ | 「モデル蒸留で KL を使う目的は?」 | 予測分布のズレを最小化し軽量化後の品質を維持するため | “ズレ最小化=品質維持”のキーワードで瞬時に答える |
暗記フック
- 対称=×、0 以上=○――2語で判定を自動化
- H+KL=Cross――“H(本体)に KL(余計)が付くと交差エントロピー”と語呂で覚える
本番そっくり!ミニ模試5問
- DKL が 0 になるのはどのような場合ですか?
A) P と Q が独立 B) P = Q C) Q が一様分布 - DKL(P‖Q) と DKL(Q‖P) が等しいのは常に真か?
○ / × - 交差エントロピーを最小化すると同時に最小化される量は?
A) H(P) B) DKL(P‖Q) C) H(Q) - データドリフト検知で KL を使うとき、本番分布をどちらに置くべきか?
A) P B) Q - DKL の三角不等式に関する記述として正しいものは?
A) 必ず成り立つ B) 必ず成り立たない C) 一部条件下でのみ成り立つ
60秒で得点率を底上げする“当日テクニック”
- 式問題は「分子P・分母Q・正符号」だけに目を凝らす
- 距離・対称・三角不等式という単語が出たら 90%は×
- シナリオ問題は“ズレを測る/最小化する”をキーワードに回答文を構成
- 時間がなければ数学問題より○×判定を先に消化し得点を積む
一夜漬けフレーズ集(声に出して3回)
- 「エントロピーに余計コストが付くと交差エントロピー」
- 「KLは対称じゃない、0以上、距離じゃない」
- 「本番をP、学習をQ」
この章を読み終えた今、あなたはKLダイバージェンスの定義・特徴・応用例・試験対策をワンパッケージで掌握しました。
次章ではアウトプット力を高めるため、Python実装→可視化→ビジネス報告資料作成までをステップバイステップで解説します。
Python実装でKL情報量を計算・可視化しビジネス報告資料に落とし込むステップバイステップ

1. ツール選定と環境セットアップ
KL情報量は scipy.stats.entropy で一行計算できますが、可視化まで視野に入れるなら NumPy/Pandas/SciPy/Matplotlib/Seaborn をインストールしておくと便利です。
pip install numpy pandas scipy matplotlib seaborn
クラウド環境に置く場合は AWS SageMaker Studio Lab や Google Colab を使うと、ライブラリプリインストールで準備時間を短縮できます。
2. サンプルデータの読み込みと分布推定
例として EC サイトの購買カテゴリ分布を学習データ(Q)、直近1週間の本番データ(P)として読み込みます。
import pandas as pd
import numpy as np
train = pd.read_csv("train_category.csv") # 学習時
serve = pd.read_csv("serve_category.csv") # 本番
# カテゴリごとの度数 → 確率に正規化
Q = train['category'].value_counts(normalize=True).sort_index().values
P = serve['category'].value_counts(normalize=True).reindex(train['category'].unique(), fill_value=0).values
reindex+fill_value=0 で “本番にだけ出現した新カテゴリ” をゼロ埋めし、次のステップで 0 割防止のイプシロン補正を行います。
3. KL情報量の計算と安全実装テンプレート
from scipy.stats import entropy
def safe_kl(p, q, epsilon=1e-12):
p = np.clip(p, epsilon, 1)
q = np.clip(q, epsilon, 1)
p /= p.sum(); q /= q.sum() # 念のため再正規化
return entropy(p, q)
kl_value = safe_kl(P, Q)
print(f"DKL(P‖Q) = {kl_value:.4f}")
- ゼロ割り対策:
np.clipで極小値を加算 - 正規化二重チェック:合計が1 になるよう再スケール
- 印刷結果:数値が 0.05 を超えたら再学習トリガー、などビジネスルールに合わせて閾値を設定します。
4. ヒートマップで「どのカテゴリがズレたか」を経営陣へ可視化
数値だけでは伝わりづらいので、カテゴリ別の差分をヒートマップにすると報告資料で一瞬で意図が伝わります。
import matplotlib.pyplot as plt
import seaborn as sns
diff = P - Q
plt.figure(figsize=(10,1))
sns.heatmap(diff[np.newaxis, :],
cmap='coolwarm',
annot=True,
cbar=False,
xticklabels=train['category'].unique())
plt.yticks([])
plt.title('Category Drift (P - Q)')
plt.show()
- 赤色:本番で急増→品切れリスク
- 青色:本番で急減→在庫過多リスク
このビジュアルを経営会議スライドに貼ると、“見て3秒で意思決定” が可能になります。
5. レポーティングテンプレートをワンショット生成
『モデル健全性レポート』要約例
| 指標 | 今週 | 先週 | 閾値 | 判断 |
|---|---|---|---|---|
| KLダイバージェンス | 0.062 | 0.041 | 0.05 | ★ 再学習推奨 |
| 精度(AUC) | 0.842 | 0.856 | - | 経時劣化傾向 |
- 結論:KL が閾値超過、カテゴリ A・F で分布シフト顕著。
- 提案:学習データに直近 1 か月を追加し 24 時間以内に再学習。
- 効果:リコメンド誤配信による売上ロス想定 7.2% を回避。
6. 資格試験に活かすアウトプット術
- 今回のコードを Qiita に投稿し、「KL 情報量でデータドリフト検知」 タグを付与。
- ポイントは「ε 補正」「非対称性の向き」など頻出論点を本文に盛り込む。
- 投稿 URL をポートフォリオに載せると、E 資格の実装課題や転職で強力なアピール材料になります。
ここまでの実装チャプターで得たもの
- KL計算→可視化→レポーティングの一気通貫フロー
- 自社データへ即転用できる安全テンプレート
- 資格試験だけでなくビジネス報告でも説得力を倍増させるアウトプット術
次章(最終章)では、KLダイバージェンス習得を AI資格合格とキャリアアップ にどう結びつけるかを総まとめし、明日から行動に移すチェックリストを提示します。
まとめ|カルバック・ライブラー情報量を武器にAI資格もキャリアもレベルアップ

カルバック・ライブラー情報量(KLダイバージェンス)は「確率分布間のズレ」を測る万能の物差しです。
G検定・E資格などAI資格の得点源になるだけでなく、データドリフト検知や異常検知、生成AI評価などビジネス実装の現場でも即効性があります。
ここでは本連載のポイントを振り返り、明日から実行できるアクションをチェックリストにまとめます。
本記事で押さえた5つの到達点
- 定義と直感の一体化
- バケツの水位メタファで「余計に払う情報コスト」をイメージ。
- 5大特徴を瞬時に判別
- 非対称・非負・距離でない・三角不等式不成立・交差エントロピーとの和分解。
- 実践活用フレーム
- データドリフト閾値設定 → 再学習トリガー → 売上ロス抑制。
- 試験頻出パターン完全攻略
- ○×・式選択・応用シナリオの4タイプをテンプレ解法で時短。
- Python一気通貫テンプレート
- 安全計算 → ヒートマップ可視化 → 経営レポート自動生成。
明日から動くチェックリスト
| ToDo | 期限 | 完了 |
|---|---|---|
| [ ] 公式シラバスでKL関連セクションを再読しキーワード付箋を作成 | 今日 | ☐ |
[ ] safe_kl() テンプレートを自社データで動作確認 | 今週 | ☐ |
| [ ] 週次ジョブでKLトレンドを自動描画しダッシュボードに追加 | 今週 | ☐ |
| [ ] Qiita・Noteに記事「KLでドリフト検知」を投稿 | 来週 | ☐ |
| [ ] G検定過去問のKL分野をタイマー90秒/問で再演習 | 来週 | ☐ |
最後に――資格と実務をつなぐ黄金ループ
- 資格学習で理論を仕入れる
- 実務データでPython実装し可視化する
- 成果を社内外へ発信する
- フィードバックを受けて次の上位資格へ挑戦する
このループを3巡させれば、AI資格のロゴが“ただの肩書き”から“ビジネスを動かす証明”へ変わります。
KL情報量はその起点にして最強のレバレッジ。
今日からチェックリストを実行し、AI資格合格とキャリアのアップグレードを同時に手に入れましょう。
ちなみに無料で使えるG検定の理解度チェックアプリがあります。
>まずはこちらからあなたの理解度をチェックしてみてください👇
\タダで簡単10秒!/
>今回紹介したG検定の学習内容以外を学びたい方は、こちらからご覧ください👇
